Using the Economic Order Quantity formula in inventory management

The economic order quantity model is used in inventory management to support replenishment activity, but how useful is it in reality? Can such a simple formula really be applied to today’s complex supply chains? We’ll find out in this post.

What is the economic order quantity (EOQ) formula?

Improving inventory turnover - redistributing stock

In inventory management, economic order quantity (EOQ) is the optimal reorder amount that minimises the total costs of ordering and carrying stock. The economic order quantity formula considers the cost of ordering inventory and the cost of storing it. It then identifies the order quantity where both costs are at their lowest.

The importance of the economic order quantity formula

Calculating the economic order quantity of stock items can help you reduce inventory costs. Holding costs (otherwise known as carrying costs) are the costs to store inventory and include the storage space, rent, property tax, insurance, item deterioration and obsolescence etc. Obviously, the more inventory you order and carry, the higher the holding costs will be.

Ordering costs are the costs that arise every time you order inventory. They include the costs of creating a purchase order, processing an order, receiving and inspecting the goods etc. You’ll incur ordering costs no matter the size of the order, but the more orders you place, the higher the ordering costs will be.

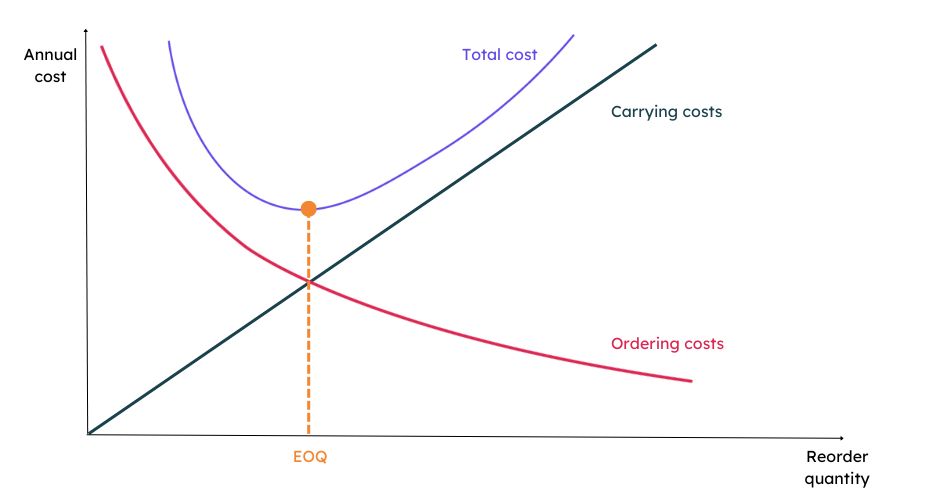
The economic order quantity calculation helps find a balance between these two conflicting costs.

How do you calculate the economic order quantity (EOQ)?

The economic order quantity formula allows you to calculate the point where your ordering and holding costs are minimised; in fact, it’s at this point where the costs are equivalent.

The graph below illustrates how the annual ordering costs and holding costs change as the reorder quantity increases; the EOQ is marked as the lowest point of the total cost line.

A working example of the economic order quantity

To calculate the economic order quantity, you need to know:

the annual demand for the item
the cost per order
the carrying cost per unit of inventory

You can then plug these numbers into the Wilson Formula, otherwise known as the economic order quantity formula:

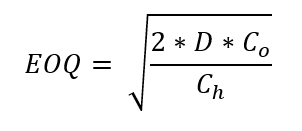
Where:

D = demand per year

C_o= cost per order

C_h = cost of holding per unit of inventory

Let’s take a look at an example of calculating EOQ:

Let’s imagine you’re a toy distributor, and one of your best sellers is a spinning top. Every year, your demand for spinning tops is 15,000. Once you factor in the cost to create, place, validate, track, and receive orders, the ordering costs come to £20 per order. Finally, the holding cost for each spinning top – including rent, storage space, insurance, etc. – ends up at £0.50 per unit.

D = 15,000

C_o= £20

C_h = £0.50

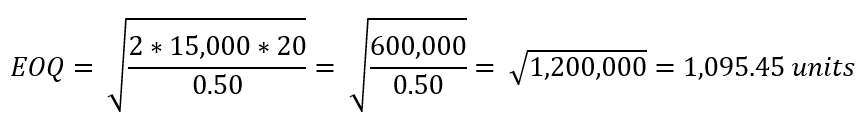
This means that the EOQ for spinning tops is approx. 1,096 units per order. With an annual demand of 15,000 units, you’ll be placing orders with your supplier approx. 14 times per year.

Assumptions when calculating economic order quantity (EOQ)

Whilst the economic order quantity formula is a relatively simple way to calculate your reorder points, there are several factors to consider when using it:

How consistent is your demand? If it varies considerably, ordering simply based on cost-effectiveness may lead to stockouts when demand rises, and excess stock when demand falls away.
Can the purchasing team and warehouse staff manage the frequency of orders recommended by EOQ calculations?
Do your inventory items vary in value and importance to the business? If the answer’s yes, maybe their reordering parameters should not all be the same.
If you have minimum order quantities to hit with certain suppliers, ordering based on the EOQ may not be possible.
Are your suppliers’ lead times always to schedule? If not, you may need to regularly adjust safety stock levels to prevent stockouts when deliveries are late.

For more details about these assumptions, read our post, the problem with the economic order quantity model.

Making the economic order quantity formula work for your business

If you decide to base your reordering processes on EOQ calculations, you need to ensure you’re constantly monitoring and updating the data you input into the formula, e.g. demand, cost per order and holding costs.

You also need to be sure that your internal operations and supplier network are happy to accommodate the number of orders stipulated in the calculations’ results.

Without software to support it, manually calculating the economic order quantity for potentially thousands of SKUs will be very time-consuming. It will also inevitably lead to errors in replenishment and, consequently, stockouts or excess inventory levels. You may, therefore, want to find an inventory management solution or enterprise resource planning (ERP) platform that will calculate EOQ for you.

An alternative to economic order quantity calculations

If you’d like to overcome the limitations of using the EOQ model and investigate alternative ways of calculating your reorder points and quantities, you could consider investing in an inventory optimisation tool, such as EazyStock. EazyStock will tell you what to order and when, basing calculations on a range of supply and demand variables, including:

Demand forecasts – which take into account demand volatility, an item’s position in its product lifecycle, seasonality and trends.
Supplier lead times – automatically adjusting reorder quantities to cover variable lead times
Current stock – which includes stock in the warehouse (or warehouses), stock on order and in transit, and safety stock levels.
Supplier restrictions – including min/max order quantities.

For more information or to book a free demo, contact us today.